¡Aquí encontrarás todo lo relacionado con las leyes del Seno y Coseno!

¡HOLA BLOGUEROS!

ESTE BLOG FUE ELABORADO POR LOS ESTUDIANTES DE LA MODALIDAD ACADÉMICA DEL GRADO 10-3 DE LA INSTITUCIÓN FRANCISCO TORRES LEÓN PUENTE AMARILLO (RESTREPO, META)

⌁Juan Felipe Triana Suárez

⌁Maicol Herrera Mancera

⌁Dylan Mosquera Villar

⌁Samuel David Corredor Caicedo

PARA MÁS INFORMACIÓN CONTÁCTANOS A NUESTRO CORREO:

Correo electrónico: themaiik10x@gmail.com

En este blog te enseñaremos a solucionar triángulos oblicuos utilizando las leyes del Seno y del Coseno, en primer lugar verás una breve introducción a cada una de las leyes y posteriormente ejercicios con sus respectivas respuestas.

ÍNDICE

Ley Seno

Ley Coseno

Ejercicios

Videos

LEY SENO

¿Qué es?

La ley de los senos es la relación entre los lados y ángulos de triángulos no rectángulos (oblicuos). Simplemente, establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado.

Fórmula:

EJEMPLOS:

Para usar la ley de los senos necesitas conocer ya sea dos ángulos y un lado del triángulo (AAL o ALA) o dos lados y un ángulo opuesto de uno de ellos (LLA).

Primer ejemplo con (AAL):

→ Solucionaremos el siguiente triángulo (△ABC):

» Primero debemos hallar el Ángulo C y se hace de la siguiente manera:

C = 180° – A – B

C = 180° – 30° – 20 ° = 130°

C = 130°

» Luego para encontrar el valor del Lado b y el Lado c realizamos lo siguiente:

b = 30.78m

c = 68.94m

● De esta manera tendremos solucionado nuestro triángulo △ABC:

A = 30°

B = 20°

C = 130°

a = 45m

b = 30.78m

c = 68.94m

Segundo ejemplo con (ALA):

→ Solucionemos el siguiente triángulo (△ABC):

» En ambos casos de (AAL) y (ALA) primero se halla el ángulo faltante, en este caso no tenemos el Ángulo C entonces procedemos a encontrar su valor:

C = 180° – A – B

C = 180° – 42° – 75° = 63°

C = 63°

» Después hallamos el valor del Lado a:

a = 16.52cm

Y también el valor del Lado b:

b = 23.85cm

● Ahora tenemos solucionado por completo el triángulo △ABC:

A = 42°

B = 75°

C = 63°

a = 16.52cm

b = 23.85cm

c = 22cm

Tercer ejemplo con (LLA):

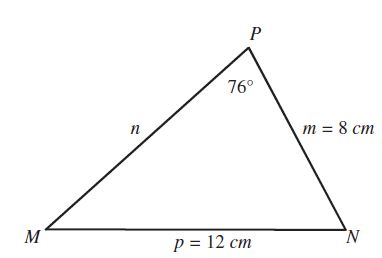
→ Solucionemos el siguiente triángulo (△MNP):

En este ejemplo a diferencia del anterior, no disponemos de dos ángulos. Solamente tenemos dos lados, por lo cual no podemos restar los dos ángulos internos con 180, e iniciar el proceso como se hizo anteriormente. En estos casos se debe utilizar la siguiente fórmula:

» Primero debemos tomar el par de lado y ángulo que tengamos y utilizando la fórmula anterior para encontrar otro ángulo:

» Organizamos los valores de igual manera que en los ejercicios anteriores, pero debemos multiplicar la fórmula por seno inverso, con esto podemos sacar el valor del ángulo M:

M = 40° 18' 20''

» Ahora que ya tenemos el ángulo terminamos el ejercicio de igual manera que los demás:

N = 180° – P – M

N = 180° – 76° – 40° 18' 20''

N = 63° 41' 40''

» Luego para encontrar el valor del Lado n realizamos lo siguiente:

n = 11.08 cm

● Ahora tenemos solucionado por completo el triángulo △MNP:

M = 40° 18' 20''

m = 8 cm

N = 63° 41' 40''

n = 11.08 cm

P= 76°

p = 12 cm

LEY COSENO

¿Qué es?

La ley de los cosenos es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluido son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas.

Fórmulas (hallar lados):

c 2 = a 2 + b 2 – 2 ab cos C.

b 2 = a 2 + c 2 – 2 ac cos B.

a 2 = b 2 + c 2 – 2 bc cos A.

Formulas (hallar ángulos):

EJEMPLOS:

Primer ejemplo con (LAL)

→ Solucionaremos el siguiente triángulo (△ABC):

» Primero debemos acomodar los datos en la fórmula presentada anteriormente y para eliminar el exponente de la c debemos utilizar la raíz cuadrada en la operación, así encontraremos el valor del Lado c: